Categorical Syllogism, Venn Diagrams and Rules for Testing for
Validity
Major Term, Minor Term, Middle Term,
Major Premise and Minor Premise
Categorical
Syllogisms and “Standard Form.”
The Mood of a
Categorical Syllogism
The Figure of a
Categorical Syllogism
Testing for
Validity Using the Rules
Diagramming Syllogisms: Six Steps
A Last Point About the Diagrams
Major Term, Minor Term, Middle Term,
Major Premise and Minor Premise
A Categorical Syllogism is a two premised deductive argument whose
every claim is a categorical claim, and in which exactly three terms appear in
the argument. Each term occurs exactly
twice. Two terms appear in the
conclusion and one term does not appear in the conclusion at all, but only in
the premises.
Example:
Some consumers are not
Democrats.
All Americans are consumers.
Therefore
Some Americans are not Democrats
Notice:
Each
of the three terms appear exactly twice in exactly two claims. The terms are to be labeled in the following
way.
1. Major Term: The term that
appears as the predicate in the conclusion of the argument is call the major
term.
2. Minor Term: The term that
appears as the subject in the conclusion of the argument is called the minor
term.
3. Middle Term: The term that
appears in both premises of the argument but not in the conclusion is
call the middle term.
4. Major Premise: The premise which
contains the major term is the major premise.
5. Minor Premise: The premise which contains the minor
term is called the minor
premise.
In a
Standard Form Categorical Syllogism, the Major Premise goes on top
of the Minor Premise.
So:
Take
our Example:
Some consumers
are not Democrats.
All Americans
are consumers.
Therefore
Some Americans
are not Democrats.
Major Term (i.e.
Predicate of the conclusion)
Minor Term (i.e.
Subject of the conclusion)
Middle Term (i.e.
not in the conclusion)
Major Premise (Above the minor
premise)
Minor Premise (Underneath the
major premise)
|
Quantifier |
Subject |
|
Predicate |
|
|
Some |
Consumers |
are not |
Democrats. |
Major Premise |
|
|
Middle Term (i.e. not in
the conclusion) |
|
|
|
|
All |
Americans |
are |
consumers. |
Minor Premise |
|
Therefore |
|
|
Middle Term (i.e. not in
the conclusion) |
|
|
Some |
Americans |
are not |
Democrats. |
|
|
|
Minor Term (i.e. Subject of the
conclusion) |
|
Major Term (i.e. Predicate of the
conclusion) |
|
The
most frequently use symbols used to abbreviate these terms are P, S, and M.
P for the major term
S for the minor term
And
M for the middle term.
Categorical
Syllogisms and “Standard Form.”
For a
categorical syllogism to be in “Standard Form” the Major Premise must be on top.
And the Minor Premises must be under the Major Premise.
So notice:
All Americans
are consumers.
Some consumers
are not Democrats.
Therefore
Some Americans
are not Democrats.
Is NOT
in standard form, The minor premise in
on top.
While
this argument is logically identical to the one above, this rendering of the
argument is NOT is standard form.
The minor premise is one top. The
“Mood” (See below.) of this argument is OAO, NOT AOO. Likewise, this argument is in 1st
figure, not 4th figure. (See
below.) Failing to put the syllogism
into standard form, therefore, can be visually misleading.
The Mood of a
Categorical Syllogism
Once
a categorical syllogism is in standard form, we can then
determine its mood. One aspect of the
form of the syllogism is named by listing its “mood.” The Mood of the syllogism we are considering
here is OAO. That is, the major premise is an O claim, the
minor premises is an A claim, and the conclusions is an O claim. Hence, OAO.
Now
suppose the argument was presented this way:
All Americans are consumers.
Some consumers are not Democrats.
therefore
Some Americans are not Democrats
You
might think the mood of the syllogism is AOO. But you would be wrong. Why? You would have been fooled into thinking
this because the syllogism is NOT in
standard form here. This is because the
Minor Premise is on top and the Major premise is
underneath. So
to know what the Mood of the syllogism is, one must be certain that the syllogism is in
Standard From
The Figure of a
Categorical Syllogism
Once
a categorical syllogism is in standard form, we can then
determine its figure. The figure of a
categorical syllogism refers to the arrangement of the middle terms in the
premises. The middle terms can be arranged in four possible ways. They are:
|
M P |
R M |
M P |
P M |
|
S M |
S M |
M S |
M S |
|
S P |
S P |
S P |
S P |
The
“shirt collar” mnemonic device can be used to remember the four possible
figures. The Ms (middle terms) line up
as if on the edges of a shirt collar.
|
M P |
R M |
M P |
P M |
|
S M |
S M |
M S |
M S |
|
S P |
S P |
S P |
S P |
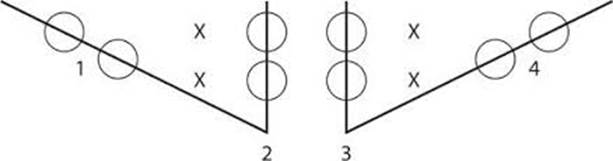
So notice:
Some consumers
are not Democrats.
All Americans
are consumers.
Therefore
Some Americans
are not Democrats.
Since
the middle terms line up on a diagonal that goes from upper left to lower right,
it is in “1st” figure.
Now
suppose the argument was presented this way:
All Americans are
consumers.
Some consumers
are not Democrats.
therefore
Some Americans
are not Democrats.
Here
it appears that the middle terms line up on a diagonal that goes from upper
right to lower left, and thus that it is in “4th” figure. You might think this because the syllogism is
NOT in standard form here. This is because the Minor Premise is on top and the Major premise is underneath. So, to know what the figure of the syllogism
is, one
must be certain that the syllogism is in Standard From
·
Mood and Figure can be used to classify all possible categorical
syllogisms.
·
Note there are four different types of categorical claims, and
each syllogism contains a total of three.
So there are only 64 different possible Moods. (e.g. AAA, AAE, AAI,
AAO, AEA, AEE, AEI, AEO, etc.)
·
Each mood can be configured in four different figures. That means there are only 256 possible
standard form categorical syllogisms.
·
Of the 256, only 24 are valid forms.
·
Of the 24 valid forms, 15 are unconditionally valid, and 9 are
conditionally valid. (More on this below.)
Testing for
Validity Using the Rules:
Five
rules apply to determine whether a syllogism is unconditionally valid:[1]
(If a
syllogism does not violate rules 1-5, but does violate rule #6, it is said to
be conditionally valid.)
Rule 1:
In a valid categorical syllogism, the middle term must be distributed in
at least one premise.
Rule 2:
In a valid categorical syllogism, any term that is distributed in the
conclusion must be distributed in the premises.
Rule 3:
In a valid categorical syllogism, if the argument has a negative
premise, it must have a negative conclusion.
Rule 4:
In a valid categorical syllogism, if the argument has a negative
conclusion, it must have a negative premise.
Rule 5:
In a valid categorical syllogism, there cannot be two negative premises.
Rule 6:
(Conditional Requirement) In a valid categorical syllogism, a particular
conclusion cannot be drawn from two universal premises. (If one assumes
existential import, the argument may be conditionally valid.)
All
and only those arguments that pass each of these tests are valid. This is a conjunctive test. Failure to satisfy one or more of the rules
renders the argument invalid.
So notice, in many cases, once I know the mood
and figure of the argument in question, I can determine whether it is valid
quite easily. For instance:
·
No argument with the Mood of EEE is valid regardless of
figure. (Why? Fails rule 5.)
·
No argument with a mood of III is valid. (Why? Fails Rule 1)
·
No argument of the mood AAE is valid. (Why? Fails
rule 4)
and
so on.
So,
to test for validity, I suggest you
1. Plot out your
argument by mood and figure.
2. Underline any
terms that are DISTRIBUTED
3. Apply the rules:
Example:
AAA 1st
Figure
Mood
tells us…
All __ are __
All __
are __
All __ are __
Figure
Tell us …
All M are __
All __
are M
All __ are __
Plug
in Major and Minor Terms
All M are P
All S are M
All S are P
Underline
distributed terms.
All M
are P
All S
are M
All S
are P
Now
rule check.
Rule 1 Check
Rule 2 Check
Rule 3 Check
Rule 4 Check
Rule 5 Check
Rule 6 Check
AAA 1st
Figure is Valid. Indeed, it is
unconditionally valid.
How
about AAA 2nd Figure?
All P are M
All S are M
All S are P
Rule 1 Failed (M is
not distributed.)
Rule 2 Check
Rule 3 Check
Rule 4 Check
Rule 5 Check
Rule 6 Check
No,
it is invalid.
How
about AAI 1st Figure?
All M are P
All S are M
Some S are P
Rule 1 Check
Rule 2 Check
Rule 3 Check
Rule 4 Check
Rule 5 Check
Rule 6 Failed
Thus
AAI 1st Figure is conditionally valid. That it, if we know or can assume that there
is at least one S, in other words, make the existential assumption, then we can
regard the argument as valid. The
premises would give us good reason to accept the conclusion.
Of
the 256, only 24 are valid forms. Of the 24 valid forms[2],
15 are unconditionally valid, and 9 are conditionally valid.
Unconditionally valid
|
Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
|
|
|
AAA |
AEE |
AII |
AEE |
|
Conditionally valid
|
Figure 1 |
Figure 2 |
Figure 3 |
Figure 4 |
Required condition |
|
AAI |
AEO |
AEO |
S exists |
|
|
AAI |
EAO |
M exists |
||
|
AAI |
P exists |
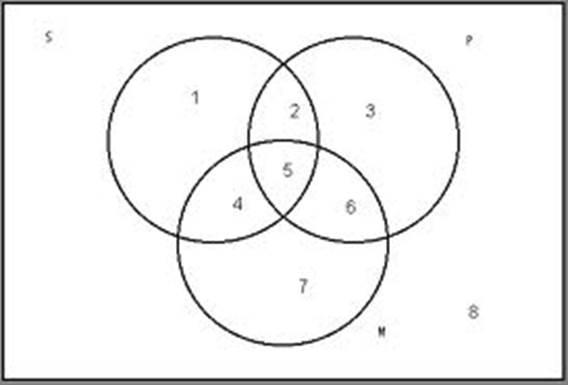
Since categorical syllogisms have three categories
the Venn diagram needed to graph a categorical syllogism will require three
circles. We will be using this configuration in our class.
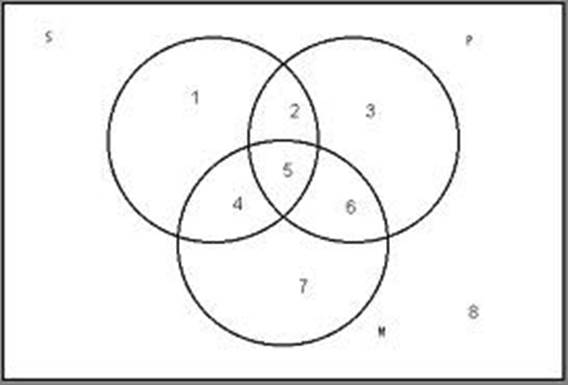
We
must first draw three overlapping circles.
To keep our diagrams uniform and representative of the actual relations
between the claims, we make the upper two circles represent the S (minor term) and
P (major term) and the middle circle represent the class of the M (middle term). This renders a diagram with seven distinct
regions. The S category includes regions 1,2,4, and 5. The P category includes regions 2,3,5 and
6. And category M includes 4,5,6, and 7.
Diagramming Syllogisms: Six Steps
Step One
1. Draw the three
overlapping circles.
Step Two
2. Identify the
minor term, the major term, and the middle term.
Step Three
3. Label the minor
term as the upper left-hand circle, the major term as the upper right-hand
circle, and the middle term as the bottom center circle.
Step Four
4. Determine whether
you need to shade and whether you need to place an X. Universals require shading; particulars
require placing an X.
Step Five
5. Shade whatever
needs to be shaded first. Then,
afterwards, place an X if the argument contains a particular premise.
Step Six
6. Put your pencil
down.
You
do not diagram the conclusion.
Rather
you only diagram the major and minor premises. The whole idea is that once you
diagram the major and minor premises, if the argument is valid, the conclusion
will be diagrammed for you. If the
argument is invalid, the conclusion will NOT be diagrammed for you. But to be clear you do not diagram the conclusion
directly; you only diagram the premises.
Let's
diagram the following syllogism.
No Republicans are
collectivists.
All Socialists are
collectivists.
therefore,
No Socialists are Republicans.
In
this example:
Step One
1. Draw the three overlapping
circles.
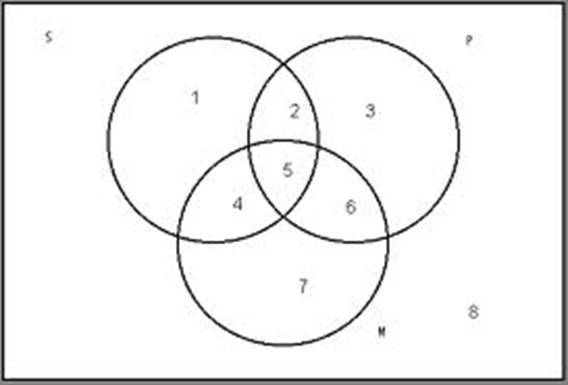
Step Two
2. Identify the
minor term, the major term, and the middle term.
Socialists is the Minor term
Republicans the Major term
Collectivists the Middle
Step Three
3. Label the minor
term as the upper left-hand circle, the major term as the upper right-hand
circle, and the middle term as the bottom center circle.

![]()



Step Four
4. Determine whether
you need to shade and whether you need to place an X. Universals require shading; particulars
require placing an X.
Since
both premises are universal, here we only have to
shade.
Step Five
No R are C means that regions 5 & 6 are shaded.

![]()



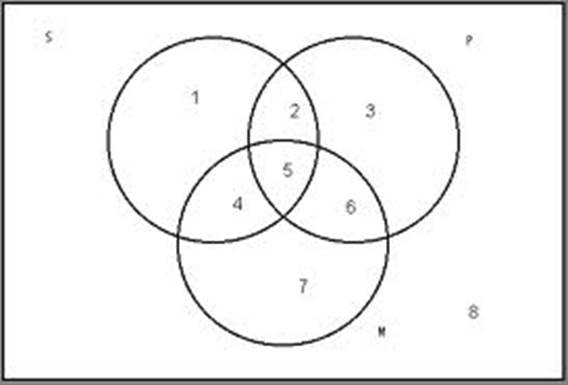
All
Socialists are Collectivists means that region 1 and 2
are shaded.




So,
when you do both, regions 1,2,5, & 6 are shaded.





Step Six
5. Put your pencil
down.
Now
the conclusion is: No Socialists and Republicans. If true, regions 2& 5 would be empty/
shaded.
And
they are already. In other words, the
truth of the premises entails the truth of the conclusion, and this is a valid
syllogism.
Placing an X
When
one or more of the premises is an I or an O-claim, by shading first we can
determine where the X need to go.
No P
are M
Some S are M
Some S are not P
No P
are M means that regions 5 and 6 are shaded/ empty.
Some
S and M means that an X need to go in the intersection of circle S and circle M
(i.e. regions 4 & 5).
But
it can’t be region 5 because we have already determined that region 5 is empty. That means that the only place for the X to
go is region 4.
Then
we put our pencil down.
The
conclusion states “Some S are not P.” This means that there needs to me an X in
either region 1 or region 4. And there
is. We know that there is an X in region
4 and thus we know that some S is not P.
In other words, the truth of the premises entails the truth of the
conclusion, and this is a valid syllogism.
But
other times there can be a problem about where to put the required X. The following example represents such a
problem.
All P are M
Some S
are not M
therefore,
Some S
are not P
All P
are M means we shade regions 2 & 3.
Some S are M means we have to place an X in the intersection
between the S circle and the M circle.
But should it go in region 4 or region 5? We don’t know. We would have to place it on the line between
the two, but that means we really don’t know if either section is
occupied or not.
Now
we put the pencil down.
The
conclusion states that some S are not P. For us to know that this is true, we would
have to have a X appear unambiguously in either region 1 or 4. But we don’t have this. The truth of the premises does not entail the
truth of the conclusion, and this is an invalid syllogism.
A last point about the diagrams
When
both the premises are universals, but the conclusion is a particular claim where
does the X come from? Well, this depends
on what type of Square of Opposition you are using. Put another way, are you going on the
assumption that you are dealing with non-empty sets, or
are you accepting the possibility that one or more of the sets about which you
are talking are empty.
On
the hypothetical interpretation of universal, no argument is valid which goes
from exclusively universal premises to a particular conclusion. There is no place for the “X” to come
from. However, on the existential
presupposition, if any circle has all but one area shaded in, an X should be
placed in that remaining area. If the
set is not empty, then the only place for members to be is that last unshaded area. For that reason, you are justified in placing
the X in the last free area.
1) Translate into
Standard Form Categorical Claims
2) Identify Terms
3) Put in Standard
Form Syllogism and Underline Distributed Terms
4) Identify Mood and
Figure
5) Rules Test for
Validity
6) Diagram Test for
Validity
Plain
English sentence:
There are legal limits on all gamefish, but
carp are not gamefish. So, there are no legal limits on carp.
1) First translate
to standard form categorical claims:
There are legal limits only on gamefish.
Since carp are not gamefish.
Therefore:
There are no legal limits on carp,
All Gamefish are Fish with legal limits.
No Carp are Gamefish.
Therefore:
No Carp are Fish with legal limits.
2) Second identify
terms
Major Term: (L)
Fish with Legal Limits
Minor Term: (C)
Carp
Middle Term: (G)
Game Fish
3) Put in a Standard
Form Categorical Syllogism
All Gamefish (G) are (L) Fish with legal
limits.
No Carp (C) are Gamefish (G).
No Carp (C) are Fish with legal limits (L).
All G are L.
No C are G.
No C are L.
4) Identify Mood and
Figure
Mood
and Figure: AEE 1
5) Rule Check
|
Check |
Rule 1: In a valid
categorical syllogism, the middle term must be distributed in at least one
premise. |
|
Fail |
Rule 2: In a valid
categorical syllogism, any term that is distributed in the conclusion must be
distributed in the premises. |
|
Check |
Rule 3: In a valid
categorical syllogism, if the argument has a negative premise, it must have a
negative conclusion. |
|
Check |
Rule 4: In a valid
categorical syllogism, if the argument has a negative conclusion, it must
have a negative premise. |
|
Check |
Rule 5: In a valid
categorical syllogism, there cannot be two negative premises. |
|
Check |
Rule 6: (Conditional
Requirement) In a valid categorical syllogism, a particular conclusion cannot
be drawn from two universal premises. (If one assumes existential import, the
argument may be conditionally valid.) |
6) Diagram Check
All G
are L (Sections 4 & 7 are shaded/empty.)
No C
are G (Sections 4 & 5 are shaded/empty.)
Put
pencil down
Conclusion:
No C are L (Both regions 2 & 5 should
be shaded/empty.)
But
they are not. The truth of the premises
does not entail the truth of the conclusion, and this is a invalid syllogism.